Министерство образования Российской Федерации
Новосибирский Государственный Университет
Факультет информационных технологий
Кафедра Общей Информатики
Дипломная работа
Разработка и исследование новых версий алгоритма zet заполнения пробелов в эмпирических таблицах
Рыскулов Сергей Николаевич
Научный руководитель
д. т. н., профессор Загоруйко Николай
Григорьевич
_____________________________
Новосибирск – 2005
Содержание:
Введение………………..…………………………………….……...3
1.
Обзор работ по проблеме заполнения пробелов…….….…..7
1.1
Простые алгоритмы……………….………………………..…8
1.2
Сложные алгоритмы………………………………...……….11
1.3
Алгоритм ZET…………………………………………………12
2.
Постановка задачи…………………………………………….16
3.
Алгоритм ZETBraid…………………………………………...19
4.
Результаты экспериментов…………………………………...27
5.
Заключение…………………………………………………..…33
6.
Литература……………………………………………………...34
Введение
Мерлин оправил на себе побитую молью мантию, швырнул на стол
связку ключей и произнес:
- Вы заметили, сэры, какие стоят погоды?
- Предсказанные, - сказал Роман.
- Именно, сэр Ойра-Ойра! Именно предсказанные!
- Полезная вещь - радио, - сказал Роман.
- Я радио не слушаю, - сказал Мерлин. - У меня свои методы.
А.Стругацкий, Б.Стругацкий. Понедельник начинается в субботу. История
вторая. Суета сует. Глава первая.
Анализируя информацию о деятельности каких-либо объектов
(предприятий, фирм, магазинов) по множеству показателей, которые отражают
условия производства и результаты за некоторое количество лет (месяцев, других
временных интервалов) можно найти объективные закономерности, если таблица не
является случайным набором чисел, а отражает фактические данные,
характеризующие причинно-следственные зависимости. Например, анализируя влияние
на розничный товарооборот различных факторов - объективных условий
функционирования предприятий, можно выделить следующие характеристики: темпы инфляции,
уровень доходов населения, структура расходов населения, стоимость услуг
жилищно-коммунального хозяйства, состояние промышленного и
сельскохозяйственного производства, своевременность выплаты заработной платы и
пенсий.
Такие данные собираются за 10-30 лет (в некоторых случаях в помесячной разбивке, например, при прогнозировании инфляции) по всем объектам, по которым будет проводиться прогнозирование (по всем торговым предприятиям, потребительским союзам, районам, областям). В практических расчетах приходится учитывать 500-700 различных показателей. Разумеется, подобную таблицу данных невозможно проанализировать вручную из-за ее объема и сложных причинно-следственных зависимостей. Поэтому возникла необходимость в разработке новых методов анализа и прогнозирования, к которым относятся машинные методы обнаружения закономерностей.
Рис.
1. Применение алгоритмов анализа данных
Значительная часть методов анализа данных была реализована в пакете
прикладных программ для обработки таблиц экспериментальных данных (ОТЭКС) [1],
[2]. Задачи, решаемые в пакете ОТЭКС можно разделить на несколько групп:
1) Задачи таксономии (алгоритмы FOREL, KRAB). Цель задач
таксономии заключается в разделении множества объектов на небольшое число групп
(таксонов) по «похожести».
2) Распознавание образов
(алгоритм STOLP,DRET). Распознавание можно определить как соотнесение объектов
или явлений на основе анализа их характеристик с одним из нескольких, заранее
определенных классов
3) Выбор системы
информативных признаков (алгоритм AdDel). Из множества признаков (свойств) объекта требуется выделить
признаки, влияющие на целевую характеристику объекта.
Рис.
2. Области применения алгоритмов анализа данных
4) Заполнение пробелов и
обнаружение ошибок в эмпирических таблицах (алгоритм ZET). Таблицы
экспериментальных данных часто содержат пробелы: у некоторых объектов значение
того или иного признака может отсутствовать. Задача заключается в предсказании
пустых клеток таблиц.
5) Прогнозирование
многомерных временных рядов (алгоритм LGAP).
Алгоритмы такого рода предназначены для извлечения закономерностей
(знаний) из данных и использование этих знаний для прогнозирования событий.
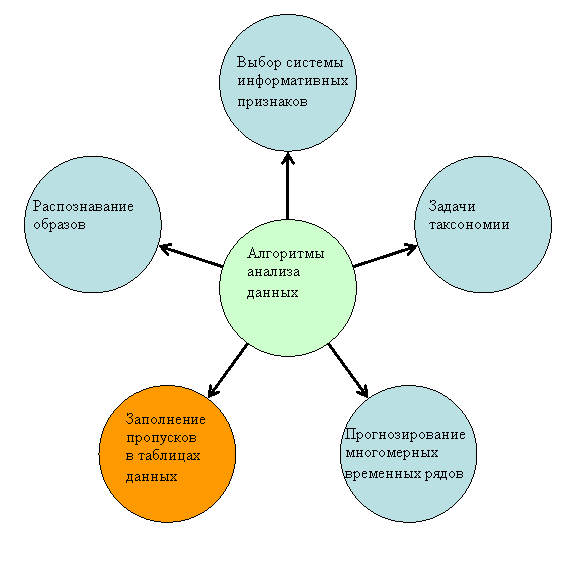
Рис.
3. Классификация задач анализа данных. Дипломная работа посвящена разработке
алгоритма заполнения пропусков в таблице данных (выделено желтым)
Первые версии пакета ОТЭКС
были сделаны более 30 лет назад. По мере появления новых вычислительных машин
делались очередные версии пакета. При этом вносились изменения в состав
программ, возникали новые программы, реализующие более эффективные алгоритмы,
совершенствовалось сервисное сопровождение пакета.
Сейчас под руководством профессора Загоруйко Н. Г, развитием проекта ОТЭКС занимаются аспирант Гуляевский С.Е., снс ктн Кутненко О.А., студенты ФИТ НГУ Рыскулов С.Н., Киселев А.Н. и другие сотрудники ИМ СО РАН и аспиранты и студенты НГУ.
Цель данной работы
заключается в разработке и исследовании новых алгоритмов заполнения
пробелов в эмпирических таблицах. В результате дипломной работы был разработан
новый алгоритм предсказания пустых клеток таблиц эмпирических данных. Этот
алгоритм является модификацией алгоритма ZET, разработанного сотрудниками ИМ СО
РАН Загоруйко Н.Г., Елкиной В.Н. и Темиркаевым В.С. При тестировании на
различных таблицах новый алгоритм дает значительное улучшение результата, по
сравнению с алгоритмом ZET и другими методами заполнения пробелов в
эмпирических таблицах.
Новый алгоритм реализован в виде программы и является частью
библиотеки прикладных программ для обработки таблиц экспериментальных данных ОТЭКС-1.
1.
Обзор работ по проблеме заполнения пробелов
Алгоритмы заполнения пробелов разрабатываются для эмпирических таблиц типа «объект-свойство». Таблицы типа «объект – свойство» - это численные таблицы, в которых в строках перечислены объекты (например, предприятия), а в столбцах - их свойства (товарооборот, уровень доходов и расходов и. т. д.). Эти таблицы экспериментальных данных могут содержать пропуски, т. е. в таблицу могут быть записаны объекты, для которых не все свойства известны. Задача алгоритмов заполнения пробелов – заполнить пропуски в таких таблицах, т. е. предсказать неизвестные значения в клетках таблиц типа «объект-свойство».
Решению задач заполнения пробелов в таблицах посвящено большое число работ [2], [3], [4], [5], [6]. Рассмотрим основные алгоритмы заполнения пропусков в таблицах данных.
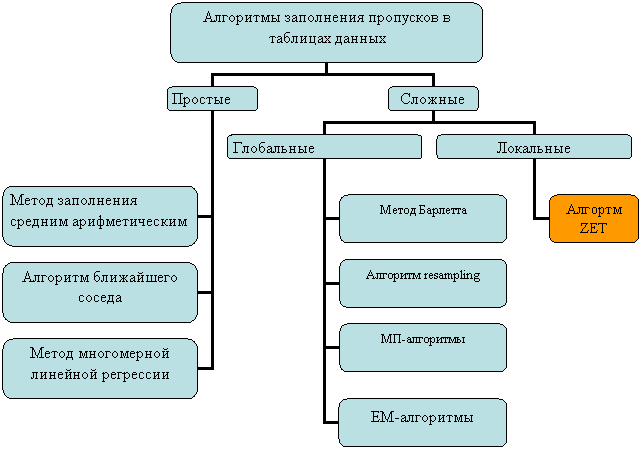
Рис. 4. Алгоритмы заполнения пробелов в эмпирических
таблицах
1.1. Простые алгоритмы
Метод заполнения средним арифметическим [3]. Это самый простой, но не самый точный метод заполнения пропусков в таблицах данных. Согласно этому методу, рекомендуется заполнять пробелы средними значениями величин, имеющихся в данном столбце.
Таким образом, неизвестное значение аij в матрице A размера N*M предсказывается
по формуле:
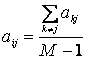
Метод К ближайших соседей. В основе алгоритма К ближайших соседей лежит предположение, что если объекты близки по значениям n-1 свойств, то они близки по значению n-ного свойства.
Заполнение пропусков в таблице данных методом К ближайших соседей
выглядит следующим образом: вначале среди всех строчек таблицы находят К
строчек, наиболее «похожих» на строчку, содержащую пробел. В качестве меры
«похожести» строчек (объектов) фигурирует декартово расстояние между строчками
в пространстве столбцов (свойств). Чем меньше декартово расстояние между
объектами в пространстве свойств, тем более они «похожи» друг на друга.
Столбец, содержащий предсказываемое значение, будем называть
целевым столбцом. Для получения предсказания неизвестного элемента значения
целевого свойства у К ближайших соседей усредняются с весами, обратно
пропорциональными из декартовому расстоянию до строки, содержащей пробел.

Где Сl – вес (компетентность) l-го ближайшего соседа, обратно пропорциональный
декартовому расстоянию rli между l-той и i-той строкой
![]()
В
частности, алгоритм одного ближайшего соседа подставляет вместо пробела
значение целевого свойства у того объекта, который больше всего похож на
предсказываемый объект.
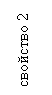
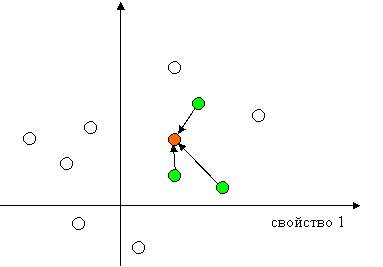
Рис
5. Иллюстрация метода трех ближайших соседей
Метод многомерной линейной
регрессии [9]. Согласно методу многомерной линейной регрессии, строится
регрессионная модель зависимости целевого свойства Y от значений свойств-столбцов X1 , … , Xn
![]()
Для получения оценок (Bi, C) параметров (bi, c) методом наименьших
квадратов нужно минимизировать по B1, …, Bn, C выражение
![]()
Сумма берется по всем объектам с известной целевой характеристикой; xij – значение i-того свойства у j-того объекта. Для получения значений параметров B1, …, Bn, C приравнивается к нулю частные производные выражения D по параметрам B1, …, Bn, С.
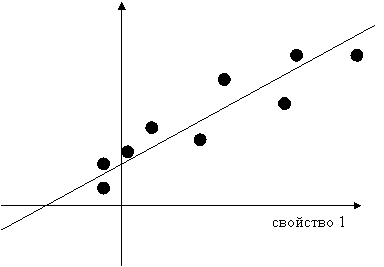
Рис 6. Пример построения уравнения линейной регрессии
1.2 Сложные алгоритмы.
Существуют и более сложные алгоритмы заполнения пробелов. Методы
Барлетта и resampling
[3] основаны на уравнениях многомерной линейной регрессии. В методе Барлетта
пропуску присваивается какое-то начальное значение (например, среднее
арифметическое столбца), затем строят уравнение многомерной линейной регрессии
с использованием начального значения пропуска, и после анализа этого уравнения
предсказывается пробел. Метод resampling является итеративным, в этом методе вместо пропуска
подставляется набор значений, и при каждом значении из этого набора строится
уравнение многомерной линейной регрессии. Все эти уравнения анализируются, и
после анализа выводится итоговое уравнение линейной регрессии, на основе которого
и предсказывается пропуск.
Существуют методы предсказания пропусков, основанные на нейросетях.
В методе главных компонент [6] ищется наилучшее приближение таблицы с пропусками матрицей вида a*ij = xi yj +bj,
где вектора x, y, b находятся итерационно. После этого
точно так же приближается матрица A-A*=(aij- a*ij), вычисляются новые вектора x (1), y (1), b (1), и т. д.,
процесс итерационно повторяется, пока все усложняющаяся модель представления
данных не будет достаточно хорошо приближать таблицу. Затем на основе этой
модели делается прогноз неизвестного элемента.
В настоящее время
интенсивно развиваются методы прогнозирования, основанные на оценках
максимального правдоподобия (МП-оценках), особенно в рамках нормальных
распределений [4]. В работе [5] предложена мощная вычислительная процедура: ЕМ-алгоритм
для решения общей задачи оценивания параметров в условиях некомплектной
выборки.
Методы, упомянутые выше,
действуют глобально: в них предполагается, что зависимость заданного (например,
линейного) типа реализована на всех объектах, поэтому и в оценивании
зависимости участвуют все строки и столбцы. Локальные алгоритмы, оценивающие
зависимости по некомплектной выборке в некоторой окрестности предсказываемого
объекта, были впервые предложены в работах [2, 7].
1.3 Алгоритм ZET
Одним из локальных алгоритмов, предназначенных для заполнения пробелов, является алгоритм ZET [1]. Изложим основные идеи этого алгоритма.
В основе алгоритма ZET лежат
три предположения. Первое (гипотеза избыточности) состоит в том,
что реальные таблицы
имеют избыточность, проявляющуюся в наличии похожих
между собой объектов (строк) и зависящих друг от друга свойств (столбцов).
Если избыточность отсутствует (как, например, в таблице случайных
чисел), то предпочесть один прогноз другому невозможно.
Второе предположение
(гипотеза аналогичности) состоит
в утверждении, что, если некоторая пара объектов близка по значениям (n-1)
свойств, то она близка
и по n-ному свойству.
Третье предположение (гипотеза локальной компетентности) заключается в том, что избыточность носит локальный характер: у каждого объекта есть свое подмножество объектов-аналогов и у каждого свойства есть свое подмножество свойств-аналогов. Если это так, то не имеет смысла привлекать к предсказанию значения некоторого элемента bij информацию, содержащуюся в строках, не похожих на i-ю строку, и в столбцах, не похожих на j-й столбец. В предсказаниях должны участвовать только т.н. "компетентные" строки и столбцы, которые выбираются для каждого предсказываемого элемента отдельно.
В работе алгоритма ZET
можно выделить три этапа.
1. На первом этапе для данного пробела из исходной матрицы "объект - свойство", столбцы
которой нормированы по дисперсии,
выбирается подмножество
"компетентных"
строк и затем
для этих строк
- подмножество "компетентных"
столбцов.
2. На втором этапе
автоматически подбираются параметры
в формуле, используемой для
предсказания пропущенного элемента,
при которых ожидаемая ошибка
предсказания достигает минимума.
3. На третьем этапе
выполняется непосредственно прогнозирование элемента по этой формуле.
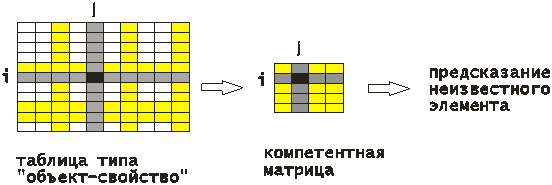
рис.
8. Этапы алгоритма ZET
Под
"компетентностью" l-той строки по
отношению к i-той
строке понимается величина
![]()
Здесь pli – величина, обратно пропорциональная расстоянию
между строками, а tli
– коэффициент комплектности, равный числу свойств, значения которых известны
как для i-й, так и для l-й строки. Компетентная строка не
должна иметь пробела в j-м
столбце.
Под компетентностью k-го
столбца по отношению к j-му
столбцу понимается величина
![]()
где pjk
– модуль коэффициента корелляции между j-м и k-м
столбцами, tij – коэффициент комплектности, равный числу объектов,
для которых известны как j-е,
так и k-е свойства.
Компетентный столбец не должен иметь пробел в i-й строке.
По указанию
пользователя программа выбирает
подматрицу любого размера в
пределах от 2*2 до n*m.
Обычно используется подматрица, содержащая от 3-х до 7-и строк и
столбцов.
В процессе предсказания значения пробела с использованием зависимостей между j-тым и всеми остальными (k-тыми) столбцами с помощью уравнений линейной регрессии вырабатываются "подсказки" bk. Если в подматрице было q+1 столбец, то q подсказок усредняются с весом, пропорциональным компетентности соответствующего столбца. В итоге получается прогнозная величина bj, порожденная избыточностью, содержащейся в столбцах:
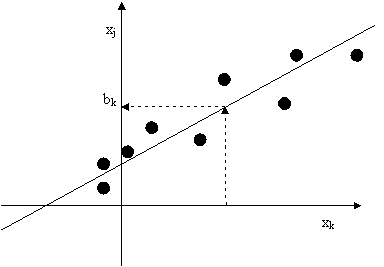
рис
9. Вычисление «подсказок» с помощью уравнения линейной регрессии
 (1)
(1)
Здесь α
- коэффициент, регулирующий
влияние компетентности на результат предсказания. При малых значениях
α разница в компетентности сказывается мало,
при больших α более
компетентные столбцы влияют гораздо больше других. Выбор α и составляет суть этапа подбора формулы для
прогнозирования: все известные элементы j-того
столбца предсказываются при разных значениях α .
Затем выбирается такое
значение α, при котором ошибка
прогноза оказалась минимальной. По формуле (1) с выбранным значением α делается прогноз bj
величины пропущенного элемента.
Процедура заполнения пробела с использованием зависимости между i-той строкой и всеми s другими (l-тыми) строками (1,2,..l...s) аналогична вышеописанной и делается по формуле

Для выбора α здесь
используются все известные
элементы i-той строки и выбор
делается при минимальном значении ошибки их предсказания. Общий
прогноз b'ij
значения пропущенного элемента
bij
получается усреднением bi
и bj.
2. Постановка задачи
Напомним, что алгоритм ZET является локальным алгоритмом, т. е. при предсказании пробела используются не все клетки таблицы, а только клетки, попавшие в некоторую окрестность предсказываемого объекта – так называемую компетентную матрицу.
Рассмотрим процесс построения компетентной матрицы в алгоритме ZET (см. рис. 10). Назовем столбец, содержащий предсказываемый пропуск, целевым столбцом, а строчку, содержащую этот пропуск, целевой строчкой. Для построения компетентной матрицы размера N*M вначале подбираются N компетентных строк, наиболее близких по декартовому расстоянию к целевой строке, затем для этих строк подбираются M компетентных столбцов. Компетентность столбца прямо пропорциональна коэффициенту корелляции между данным и целевым столбцом, причем при подсчете коэффициента корелляции учитываются только клетки столбцов, попадающие в компетентные строчки.
Такой
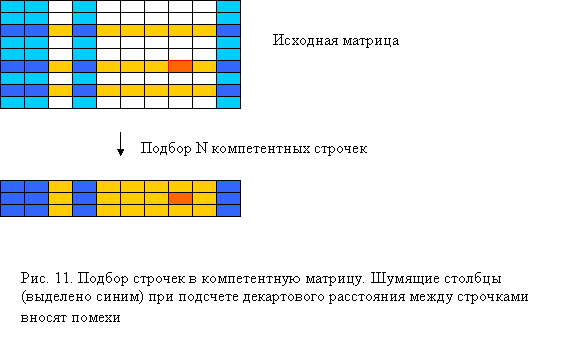
подбор компетентной матрицы имеет ряд недостатков.
A) Попадание в компетентную матрицу
неинформативных строк, и, как следствие, неинформативных столбцов. Исходная
матрица может содержать столбцы (свойства), не влияющие на целевую характеристику
(«шумящие» столбцы). Так как компетентность строки-объекта обратно
пропорциональна декартовому расстоянию до целевой строки в пространстве всех
свойств таблицы, шумящие свойства могут вносить помехи при подсчете «похожести»
строчек. Как следствие, в компетентную матрицу могут попасть неинформативные
строчки, у которых значение шумящих характеристик случайно совпало со
значениями шумящих характеристик целевой строки (см. Рис. 11).
Рис. 10. Подбор компетентной матрицы в алгоритме ZET
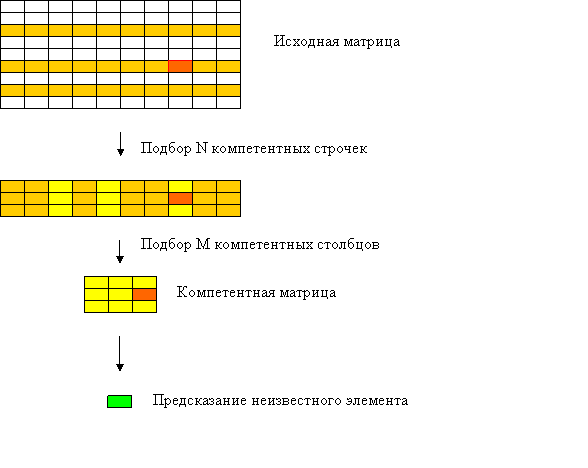
Б) Фиксированность размера компетентной матрицы. Размер компетентной матрицы в алгоритме ZET фиксирован, и обычно берут компетентную матрицу размера 7*7. Возникает вопрос, а что, если в компетентную матрицу попадут строки или столбцы, вносящие помехи в процессе предсказывания неизвестного элемента? Ведь если размер компетентной матрицы фиксирован и не зависит от таблицы, специфика таблицы может оказаться такой, что в компетентную матрицу могут не попасть строки или столбцы, хорошо предсказывающие пробел, либо могут попасть строки или столбцы, вносящие помехи.
Мы можем избавиться от этого, сделав размер компетентной матрицы
зависимым от таблицы. Для этого нам
нужно оценивать «хорошесть» компетентной матрицы, т. е. должен быть какой-то
критерий, указывающий подходит ли нам данная компетентная матрица или же мы
должны использовать матрицу другого размера.
Цель дипломной работы состоит в разработке нового метода построения компетентной матрицы, который лишен этих недостатков. В результате был изобретен новый метод подбора компетентной матрицы (метод «плетения»), о котором будет рассказано в следующей главе. Построение компетентной матрицы новым методом значительно улучшило качество алгоритма ZET. При тестировании на различных таблицах модифицированный алгоритм (ZETBraid) предсказывал неизвестные значения гораздо точнее других алгоритмов.
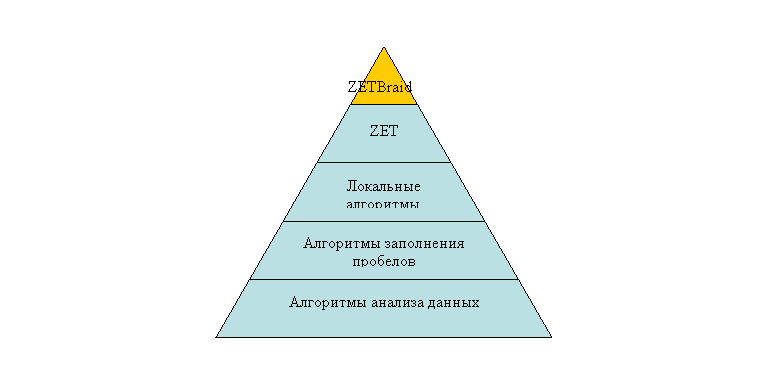
Рис.
12. Положение алгоритма ZETBraid среди других алгоритмов
3.
Алгоритм ZETBraid
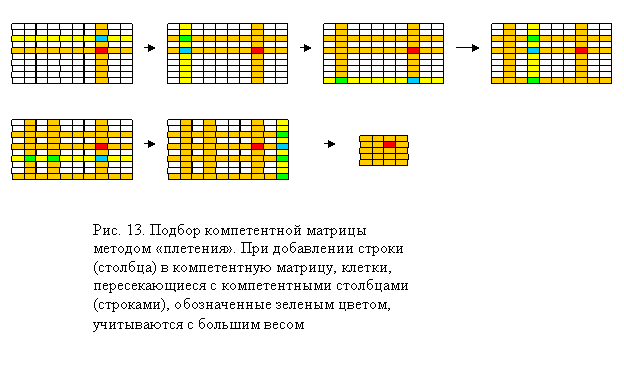
Идея алгоритма ZETBraid. Попробуем изобрести алгоритм построения компетентной матрицы, лишенный вышеперечисленных недостатков.
Для того, что бы уменьшить влияние «шумящих» столбцов при подборе компетентной строки, можно учитывать различные клетки этой строки с разными весами. При подсчете декартового расстояния между данной и целевой строкой клетки строк, принадлежащие компетентным столбцам, можно учитывать с большим весом.
В алгоритме «плетения», реализующем эту идею, строки и столбцы добавляются в компетентную матрицу по очереди – вначале в компетентную матрицу добавляется строка, наиболее близкая к целевой строке, потом – столбец, наиболее близкий к целевому, затем опять строка, наиболее близкая к целевой строке и не входящая в компетентную матрицу, и. т. д. Суть алгоритма в специфичном подсчете расстояния между строчками (столбцами) - клетки, входящие в компетентную матрицу имеют больший вес.
Столбцы матрицы перед началом работы алгоритма нормируются по
дисперсии. Компетентная матрица строится таким образом, что бы на пересечении
строк и столбцов компетентной матрицы не было пробелов (исключая тот пробел,
который мы должны предсказать).
Вычисление расстояния между строками. Расстояние между i-той и j-той строчками в матрице A=(aij) вычисляется по формуле:
![]() (2)
(2)
Где Pij равно числу столбцов,
имеющих пробел в i-й или в j-й строке, bi – некоторый весовой коэффициент,
зависящий от того, входит ли i-ый столбец в компетентную матрицу. Весовой коэффициент
должен быть таким, что бы клетки строчек, принадлежащие компетентным столбцам, имели
больший вес, нежели остальные клетки. Попробуем оценить значения коэффициентов bi.
Вычисление весов столбцов bi. Для вычисления весовых коэффициентов bj будем полагаться на три принципа:
1) Все веса столбцов,
входящих в компетентную матрицу равны
2) Все веса столбцов, не
входящих в компетентную матрицу равны
3) Сумма весов столбцов,
входящих в компетентную матрицу, деленная на сумму весов столбов, не входящих в
компетентную матрицу является константой (параметром алгоритма)
Пусть во всей матрице N столбцов, T
из них принадлежат компетентной матрице. Тогда из (1, 2, 3) следует
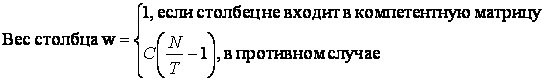 (3)
(3)
T
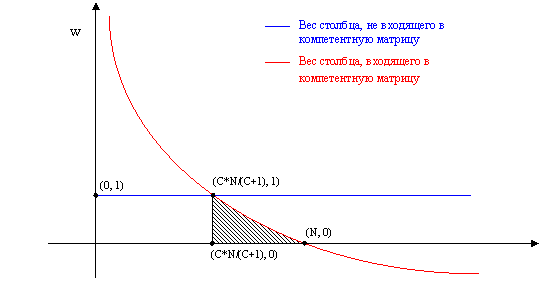
Рис 14. Вес столбца в
зависимости от количества столбцов в компетентной матрице, по формуле (3)
Как видно из графика, при числе компетентных столбцов T > C*N/(C+1)
столбцы, входящие в компетентную матрицу имеют вес меньше столбцов, не входящих
в компетентную матрицу. Что бы избавиться от этого недостатка, нужно
руководствоваться следующими правилами:
a) вес
столбца, входящего в компетентную матрицу при всех T не должен становиться меньше веса
столбца, не входящего в компетентную матрицу
b) для
того, что бы правила (1, 2, 3) хотя бы приблизительно соблюдались, вид функции w(T) должен быть примерно таким же как
раньше (3)
На основании a)
и b) предлагается сдвинуть
график C*(N/T-1)
вверх таким образом, что бы условие a) соблюдалось, причем для соблюдения b) будем сдвигать его на минимальную
величину. Таким образом, нам нужно решить систему:

Решая эту систему графически, т. е. сдвигая график C*(N/T-1) вверх, получим D=1.
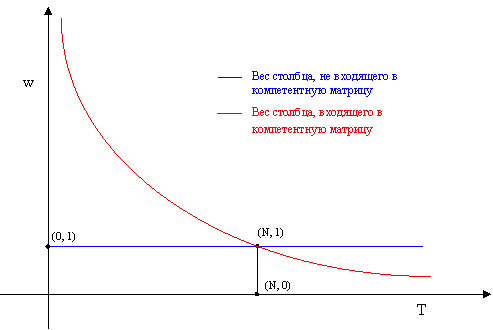
Рис 15. Вес столбца в
зависимости от количества столбцов в компетентной матрице, по формуле (4)
В результате, вес столбца w(T) вычисляется по формуле
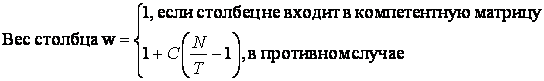 (4)
(4)
Аналогично мы поступаем с весами строк.
Предсказывая различные таблицы алгоритмами, в которых веса
вычислялись по формулам (3) и (4) см. раздел «результаты экспериментов», я не
нашел больших отличий в точности их
предсказаний. Однако при вычислении веса по формуле (4) вес столбца, входящего в
компетентную матрицу всегда ![]() веса столбца, не
входящего в компетентную матрицу. На основании этого я предлагаю вычислять вес
столбца по формуле (4).
веса столбца, не
входящего в компетентную матрицу. На основании этого я предлагаю вычислять вес
столбца по формуле (4).
Вычисления расстояния между
столбцами. Немного сложнее происходит расчет расстояния между столбцами.
Если при подсчете расстояния между строчками-объектами мы пользовались
декартовым расстоянием с учетом весов свойств, то для расчета расстояния между
свойствами нужно строить уравнение линейной регрессии. Для расчета расстояния
между столбцами X={xi} и Y = {yi} строится регрессионное
уравнение зависимости столбца Y от столбца X:
y=a+b*x.
Для нахождения коэффициентов (a, b) нужно минимизировать по (a, b) функцию:
![]() (5)
(5)
Где веса bi находятся аналогично весам клеток при подсчете расстояний между строчками
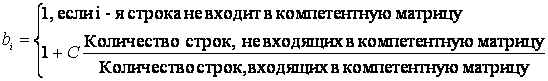 (6)
(6)
Как мы видим, при минимизации суммы отклонений от прямой a+b*x до точек {xi, yi}, отклонения от точек, входящих в компетентную матрицу учитываются с большим весом, нежели отклонения от точек, не входящих в компетентную матрицу.
![]()
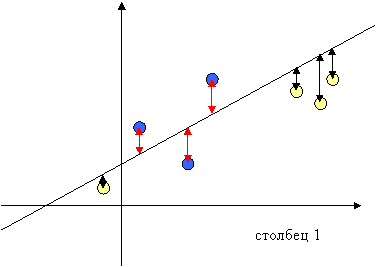
Рис 16. При
построении уравнения линейной регрессии между столбцами клетки столбцов,
входящие в компетентную матрицу (обозначено синим) имеют больший вес
Таким образом, расстояние между столбцами X и Y
вычисляется по формуле:
![]() (7)
(7)
Где Pxy равно количеству строк, имеющих пробелы в столбце X или в столбце Y, bi – весовой коэффициент, вычисляемый
по формуле (6), коэффициенты a и b вычисляются путем минимизации функции (5).
Подбор размера компетентной
матрицы. Для того, что бы автоматически подбирать размер компетентной
матрицы, поступим следующим образом. Для компетентной матрицы будем численно
оценивать ее «хорошесть», т. е. создадим критерий оценки качества
предсказывания неизвестного элемента по данной компетентной матрицы. Тогда при
построении компетентной матрицы мы будем добавлять строчки и столбцы до тех
пор, пока добавление новой строчки или столбца не будет уменьшать «хорошесть»
матрицы.
Существует два варианта оценки этой ошибки.
Согласно первому варианту (методу «креста») методом линейной регрессии предсказываются все известные значения той строки или тому столбцу компетентой матрицы, которые содержат предсказываемый элемент, и считается средняя ошибка предсказания этих значений. Таким образом, для матрицы размера n*m мы предсказываем (n-1) + (m-1) известных элементов креста компетентной матрицы, содержащего предсказываемый элемент и считаем среднюю ошибку. Эта средняя ошибка и выступает в роли оценки ошибки предсказания данной компетентной матрицы.

рис. 17. оценка
ошибки предсказания компетентной матрицы методом предсказывания известных
элементов (красным помечены клетки, которые предсказываются
Согласно второму варианту (дисперсионному методу) мы считаем дисперсию предсказаний неизвестного элемента. Методом линейной регрессии мы для каждой строки предсказываем значение неизвестного элемента, и считаем дисперсию этих n-1 подсказок. Аналогично мы считаем дисперсию m-1 предсказаний элементов по столбцам, и в качестве ошибки предсказания компетентной матрицы берем сумму полученных дисперсий.

рис.18. оценка ошибки
предсказания компетентной матрицы методом дисперсии подсказок
При тестировании на различных таблицах (см. раздел «результаты экспериментов»), дисперсионный метод оценки «хорошести» компетентной матрицы показал лучшие результаты по сравнению с методом «креста».
Прямоугольная компетентная матрица. Так как при построении матрицы методом «плетения» строчки и столбцы добавляются в компетентную матрицу по очереди, ее размер должен быть
N*N, либо N*(N-1), либо (N-1)*N. Попробуем так изменить алгоритм построения компетентной матрицы, что бы ее размер мог быть прямоугольным, вида N*M.
Для этого мы можем видоизменить алгоритм следующим образом:
1) Находим самую близкую не входящую в компетентную матрицу строку к целевой строке по метрике (2). Если добавление этой строки в компетентную матрицу не уменьшает хорошесть компетентной матрицы, добавляем ее в компетентную матрицу.
2) Аналогично, находим самый близкий не входящий в компетентную
матрицу столбец к целевому столбцу по метрике (7). Если добавление этого
столбца в компетентную матрицу не уменьшает хорошесть компетентной матрицы,
добавляем его в компетентную матрицу.
Шаги 1) и 2) повторяются до тех пор, пока мы можем добавлять к
компетентной матрице строчку или столбец.
Для того, что бы избежать ошибок при начальном построении компетентной матрицы, первые K шагов (обычно берется K=6), мы добавляем строки и столбцы в компетентную матрицу, невзирая на их влияние на хорошесть компетентной матрицы (что эквивалентно построению стартовой компетентной матрицы размера (K-[K/2])*([K/2]), к которой потом добавляются строчки и столбцы).
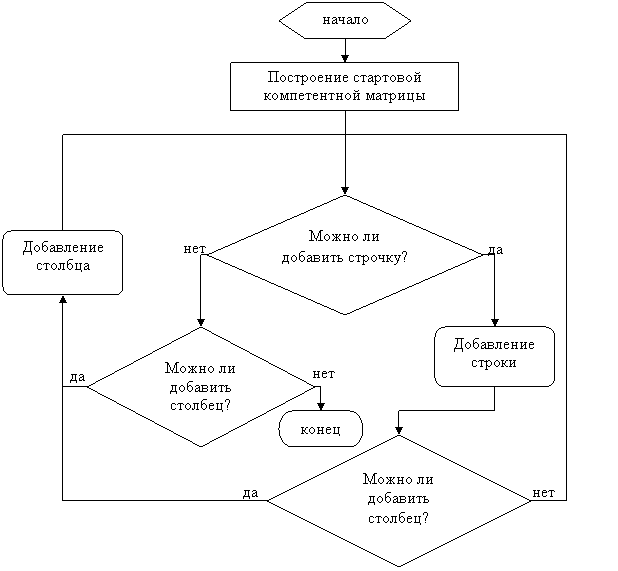
рис. 19. Подбор компетентной матрицы усовершенствованным алгоритмом «плетения»
5. Результаты
экспериментов
Метод «скользящего экзамена»
оценивания эффективности алгоритмов предсказания пробелов [1]. Пусть в
нашем распоряжении имеется набор различных стратегий (алгоритмов) F = {f1, f2, … , fv, … , ft}, предназначенных для
предсказания значений пропущенных элементов. Закроем в таблице известный
элемент b11,
стоящий на пересечении строки a1
и столбца x1,
и предскажем его с помощью всех алгоритмов F поочередно. Каждый алгоритм fv предскажет свое значение b11v, которое будет
отличаться от исходного («истинного») значения на величину d11v = |b11v-b11|.
Восстановим в таблице элемент b11, уберем элемент b12, и повторим процедуру. Получим отклонение d12v. Проделав это по очереди со всеми элементами таблицы, и просуммировав полученные отклонения, мы получим суммарную величину отклонений Dv для каждого алгоритма v. Наилучшим из них естественно считать такой алгоритм fv’, который дает минимальную сумму отклонений
![]()
В реальных таблицах данные чаще всего не нормированы, и ошибку предсказания элемента лучше всего считать в процентах
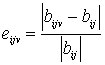
Тогда ошибку предсказывания таблицы размера N*M можно вычислять по формуле
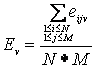
Исходные данные.
Алгоритмы заполнения пропусков тестировались методом скользящего экзамена на
следующих таблицах:
Таблица «Биоинформатика» (24 строки, 142 столбца) – таблица исследований психофизических показателей различных групп людей, полученная в результате исследования уровня тревожности
Таблица «Минэнерго» (31 строка, 14 столбцов) – таблица данных министерства энергетики США с 1970 по 2000 год
Фенотип (35 строк, 15 столбцов) – таблица исследований влияния различных медико-биологических показателей людей на заболевание сахарным диабетом.
Выбор формулы подсчета весовых коэффициентов при вычислении расстояния между строчками. Напомним, что расстояние между i-той и j-той строчками в матрице A=(aij) вычисляется по формуле:
![]()
При этом предлагалось два альтернативных варианта оценки
коэффициентов bi:
А) По формуле (3)
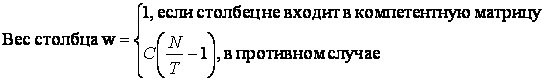
Б) По формуле (4)
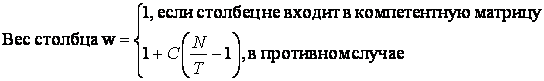
Аналогично подбираются
весовые коэффициенты при подсчете расстояний между столбцами. Для выбора, какой
из вариантов подсчета весов эффективнее, алгоритм ZETBraid был протестирован на различных таблицах с различными вариантами подбора
весов bi.
Таблица 1. Ошибка предсказания алгоритмов на различных
таблицах
|
Название
таблицы |
Значение
параметра
С |
вычисление
веса по формуле (3) |
Вычисление
веса по формуле (4) |
|
«Биоинформатика» |
С=1 |
14.97700% |
14.89990% |
|
|
С=2 |
15.29050% |
15.34290% |
|
|
С=3 |
15.50640% |
15.47580% |
|
|
С=4 |
15.56960% |
15.60230% |
|
|
С=5 |
15.71620% |
15.77730% |
|
|
С=6 |
15.73390% |
15.76960% |
|
|
С=7 |
15.96150% |
15.98190% |
|
|
С=8 |
15.93010% |
15.93330% |
|
|
С=9 |
15.95580% |
15.97620% |
|
|
|
|
|
|
«Минэнерго» |
С=1 |
2.13816% |
2.17045% |
|
|
С=2 |
2.14926% |
2.13699% |
|
|
С=3 |
2.14410% |
2.21181% |
|
|
С=4 |
2.21486% |
2.23633% |
|
|
С=5 |
2.26693% |
2.25606% |
|
|
С=6 |
2.28846% |
2.29630% |
|
|
С=7 |
2.27855% |
2.28258% |
|
|
С=8 |
2.34175% |
2.34582% |
|
|
С=9 |
2.33843% |
2.34321% |
|
|
|
|
|
|
«Фенотип»
(среднее отклонение от предсказанного значения) |
С=1 |
0.338959 |
0.293435 |
|
|
С=2 |
0.28294 |
0.261626 |
|
|
С=3 |
0.258102 |
0.235353 |
|
|
С=4 |
0.236321 |
0.256155 |
|
|
С=5 |
0.236464 |
0.236571 |
|
|
С=6 |
0.230377 |
0.263374 |
|
|
С=7 |
0.286436 |
0.287116 |
|
|
С=8 |
0.258985 |
0.264567 |
|
|
С=9 |
0.267657 |
0.276506 |
Как видно из таблицы 1, выбор способа подсчета весовых коэффициентов (по формуле (3) или (4)) слабо влияет на точность предсказания алгоритма. Однако при подсчете весовых коэффициентов методом (4) веса столбцов, входящих в компетентную матрицу всегда больше весов столбцов, не входящих в компетентную матрицу. На основании этого предлагается вычислять веса по формуле (4).
Основываясь на таблице 1, подберем значение параметра С. Так как мы решили вычислять веса по формуле (4), мы будем рассматривать значения последнего столбца таблицы 1. Заметим, что значение параметра С слабо влияет на ошибку предсказания таблицы «Биоинформатика» (14-15%) и «Минэнерго» (2.2-2.4%) и сильно влияет на ошибку предсказания таблицы «Фенотип» 0.23-0.29 (ошибка таблицы «Фенотип» мерялась не в процентах, вычислялось среднее отклонение от предсказанного значения). Исходя их этого, будем оценивать значение параметра С по таблице «Фенотип». По таблице 1, минимальная ошибка предсказания таблицы «Фенотип» при вычислении весов по формуле (4) достигается при С=3 и С=5. Далее, рассматривая влияние параметра С на предсказание таблицы «Биоинформатика», находим что при С=3 таблица «Биоинформатика» предсказывается лучше, чем при С=5. Значит, предпочтительнее всего взять значение параметра С равное трем.
Метод оценки «хорошести»
компетентной матрицы. Напомним, что для оценки качества предсказания
компетентной матрицы предлагалось пользоваться двумя методами: «дисперсионным»
и методом оценки ошибок предсказаний креста. Для того, что бы оценить какой из
этих методов лучше оба метода были протестированы на различных таблицах (см.
таблица 2).
Таблица 2. Ошибка предсказания алгоритмов на различных
таблицах
|
Название
таблицы |
Значение
параметра
С |
Дисперсионный Метод
оценки ошибки
компетентной матрицы |
Оценка ошибки
компетентной матрицы
методом «креста» |
|
«Биоинформатика» |
С=1 |
14.89990% |
15.30730% |
|
|
С=2 |
15.34290% |
16.07000% |
|
|
С=3 |
15.47580% |
16.04050% |
|
|
С=4 |
15.60230% |
16.05230% |
|
|
С=5 |
15.77730% |
16.52100% |
|
|
С=6 |
15.76960% |
16.48830% |
|
|
С=7 |
15.98190% |
16.57290% |
|
|
С=8 |
15.93330% |
16.46450% |
|
|
С=9 |
15.97620% |
16.34410% |
|
|
|
|
|
|
«Минэнерго» |
С=1 |
2.17045% |
2.56275% |
|
|
С=2 |
2.13699% |
2.47934% |
|
|
С=3 |
2.21181% |
2.44179% |
|
|
С=4 |
2.23633% |
2.43936% |
|
|
С=5 |
2.25606% |
2.41500% |
|
|
С=6 |
2.29630% |
2.46632% |
|
|
С=7 |
2.28258% |
2.42073% |
|
|
С=8 |
2.34582% |
2.41165% |
|
|
С=9 |
2.34321% |
2.42822% |
|
|
|
|
|
|
«Фенотип»
(среднее отклонение) от предсказанного значения |
С=1 |
0.293435 |
0.299832 |
|
|
С=2 |
0.261626 |
0.30689 |
|
|
С=3 |
0.235353 |
0.257968 |
|
|
С=4 |
0.256155 |
0.298016 |
|
|
С=5 |
0.236571 |
0.268363 |
|
|
С=6 |
0.263374 |
0.322892 |
|
|
С=7 |
0.287116 |
0.304086 |
|
|
С=8 |
0.264567 |
0.291732 |
|
|
С=9 |
0.276506 |
0.312962 |
На основании таблицы 2 можно сделать вывод о том, что при оценке
ошибки предсказания компетентной матрицы лучше всего пользоваться
«дисперсионным» методом.
Результаты предсказания таблиц различными алгоритмами методом скользящего экзамена. Для сравнения эффективности работы алгоритмов подстановки среднего арифметического, ближайшего соседа, ZET и ZETBraid, методом скользящего экзамена было предсказано несколько таблиц, и получены результаты:
Таблица 3. Средняя ошибка предсказания различных таблиц в
зависимости от алгоритма (ошибка предсказания таблиц «Биоинформатика» и «Минэнерго» вычислялась в процентах, таблицы «Фенотип» - в среднем отклонении предсказанного значения от
истинного)
|
Название таблицы |
Метод
подстановки среднего арифмитического |
Метод одного ближайшего соседа |
Алгоритм ZET |
Алгоритм ZetBraid |
|
«Биоинформатика» |
37,8561% |
27,9261% |
18,9558% |
15.4758% |
|
«Минэнерго» |
15,9578% |
3,83764% |
2,64802% |
2.21181% |
|
«Фенотип» |
0.882353 |
0.314286 |
0.35922 |
0.235353 |
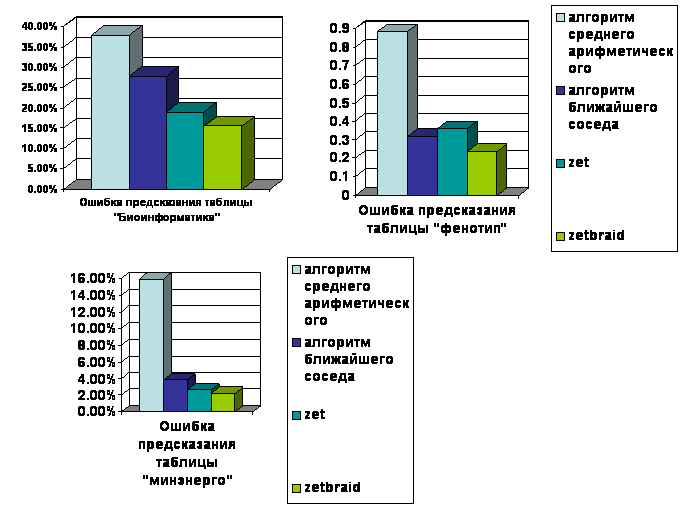
Рис. 20. Диаграммы,
иллюстрирующие зависимость средней ошибки предсказания таблиц от алгоритмов (см.
табл. 3, ошибка предсказания таблиц «Биоинформатика» и «Минэнерго» вычислялась в процентах, таблицы «Фенотип» - в среднем отклонении предсказанного значения от
истинного)
На основании таблицы 3 можно сделать вывод о том, что использование
метода «плетения» при подборе компетентной матрицы в алгоритме ZET значительно
улучшает алгоритм ZET, и
разработанный таким образом алгоритм ZetBraid гораздо точнее предсказывает неизвестные элементы
таблицы по сравнению с алгоритмом ZET и
другими алгоритмам.
6. Заключение
На сегодняшний момент задача поиска эффективных алгоритмов
прогнозирования пропусков в таблицах данных является одной из наиболее
актуальных проблем в области анализа данных. Проделанная работа стала
логическим продолжением исследований, проводимых в данной области. На базе
данных методов был создан более эффективный алгоритм, модифицированный новыми
приемами и алгоритмами в процессе исследований. Итоговый алгоритм дает
значительно улучшенный результат, по сравнению с другими подходами к
прогнозированию, и более универсален относительно характера распределения и
объема выборки, что было подтверждено экспериментально.
Новый алгоритм реализован в виде программы и является частью
библиотеки прикладных программ для обработки таблиц экспериментальных данных ОТЭКС-1.
7. Литература
1. Загоруйко Н. Г. Прикладные методы анализа данных и
знаний. Новосибирск, издательство института математики, 1999
2. Загоруйко Н. Г., Ёлкина В. Н., Емельянов С. В, Лбов Г.
С. Пакет прикладных программ ОТЭКС. М.: Финансы и статистика, 1986
3. Злоба Е., Яцкив И. Статистические методы восстановленя
пропущенных данных //Институт транспорта и связи, Рига, 2002
4.
Jaap P. L. Brand. Development, implementation and
evaluation of multiple imputation strategies for the statistical analysis of
incomplete data. //Print partners ispkamp, Enschede, 1999
5. С. А. Шумский. Байесова регуляризация обучения//IV всероссийская
научно-техническая конференция «нейроинформатика-2002», Москва, 2002
6. А.А.Россиев. Моделирование данных при помощи кривых для
восстановления пробелов в таблицах. 660036 , Красноярск- 36 , ИВМ
СО РАН, 2002
7. Загоруйко Н. Г., Ёлкина В. Н., Лбов Г. С. Алгоритмы
обнаружения эмпирических закономерностей. Новосибирск: наука, 1985
8. Двоенко С.Д. О восстановлении пропусков в данных. Тульский государственный
университет, http://lda.tsu.tula.ru/cluster/demo1_3r.htm.
9. Джонсон Н., Лион Ф. Статистика и планирование
эксперимента в технике и науке. Методы обработки данных. «Мир», Москва, 1980
10. Новоселов Ю. А.
Применение машинных методов обнаружения закономерностей в анализе,
планировании и прогнозировании социально-экономических процессов. Сибирский
университет потребительской кооперации, http://www.sibupk.nsk.su/Intranet/Univer/Info/ZET.htm